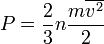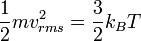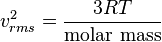Chemistry

__________________________________________________________________________


This blog provide students a study material for chemistry to prepare for Medical entrance exams in INDIA. Its source of Article and contexts is from other Organizational websites.
This is a Non-Profit organization functioning under Smas-Club

__________________________________________________________________

Kinetic theory

        




The temperature of an ideal monatomic gas is a measure related to the average kinetic energy of its atoms as they move. In this animation, the size of helium atoms relative to their spacing is shown to scale under 1950 atmospheres of pressure. These room-temperature atoms have a certain, average speed (slowed down here two trillion fold).


Kinetic theory (or the kinetic or kinetic-molecular theory of gases) is the theory that gases are made up of a large number of small particles (atoms or molecules), all of which are in constant, random motion. The rapidly moving particles constantly collide with each other and with the walls of the container. Kinetic theory explains macroscopic properties of gases, such as pressure, temperature, or volume, by considering their molecular composition and motion. Essentially, the theory posits that pressure is due not to static repulsion between molecules, as was Isaac Newton's conjecture, but due to collisions between molecules moving at different velocities.
While the particles making up a gas are too small to be visible, the jittering motion of pollen grains or dust particles which can be seen under a microscope, known as Brownian motion, results directly from collisions between the particle and air molecules. This experimental evidence for kinetic theory, pointed out by Albert Einstein in 1905, is generally seen as having confirmed the existence of atoms and molecules.

Postulates

The theory for ideal gases makes the following assumptions:
  • The gas consists of very small particles, all with non-zero mass.
  • The number of molecules is large such that statistical treatment can be applied.
  • These molecules are in constant, random motion. The rapidly moving particles constantly collide with the walls of the container.
  • The collisions of gas particles with the walls of the container holding them are perfectly elastic.
  • The interactions among molecules are negligible. They exert no forces on one another except during collisions.
  • The total volume of the individual gas molecules added up is negligible compared to the volume of the container. This is equivalent to stating that the average distance separating the gas particles is large compared to their size.
  • The molecules are perfectly spherical in shape, and elastic in nature.
  • The average kinetic energy of the gas particles depends only on the temperature of the system.
  • Relativistic effects are negligible.
  • Quantum-mechanical effects are negligible. This means that the inter-particle distance is much larger than the thermal de Broglie wavelength and the molecules are treated as classical objects.
  • The time during collision of molecule with the container's wall is negligible as comparable to the time between successive collisions.
  • The equations of motion of the molecules are time-reversible.
More modern developments relax these assumptions and are based on the Boltzmann equation. These can accurately describe the properties of dense gases, because they include the volume of the molecules. The necessary assumptions are the absence of quantum effects, molecular chaos and small gradients in bulk properties. Expansions to higher orders in the density are known as virial expansions. The definitive work is the book by Chapman and Enskog but there have been many modern developments and there is an alternative approach developed by Grad based on moment expansions.[citation needed] In the other limit, for extremely rarefied gases, the gradients in bulk properties are not small compared to the mean free paths. This is known as the Knudsen regime and expansions can be performed in the Knudsen number.
The kinetic theory has also been extended to include inelastic collisions in granular matter by Jenkins and others.[citation needed]

Factors

Pressure

Pressure is explained by kinetic theory as arising from the force exerted by gas molecules impacting on the walls of the container. Consider a gas of N molecules, each of mass m, enclosed in a cuboidal container of volume V=L3. When a gas molecule collides with the wall of the container perpendicular to the x coordinate axis and bounces off in the opposite direction with the same speed (an elastic collision), then the momentum lost by the particle and gained by the wall is:
\Delta p = p_{i,x} - p_{f,x} = 2 m v_x\,
where vx is the x-component of the initial velocity of the particle.
The particle impacts one specific side wall once every
\Delta t = \frac{2L}{v_x}
(where L is the distance between opposite walls).
The force due to this particle is:
F = \frac{\Delta p}{\Delta t} = \frac{m v_x^2}{L}
The total force on the wall is
F = \frac{Nm \overline{v_x^2}}{L}
where the bar denotes an average over the N particles. Because of the Pythagorean v^2 = v_x^2 + v_y^2 + v_z^2 , we can rewrite the force as
F = \frac{Nm\overline{v^2}}{3L}.
This force is exerted on an area L2. Therefore the pressure of the gas is
P = \frac{F}{L^2} = \frac{Nm\overline{v^2}}{3V}
where V=L3 is the volume of the box. The fraction n=N/V is the number density of the gas (the mass density ρ=nm is less convenient for theoretical derivations on atomic level). Using n, we can rewrite the pressure as
P = {2 \over 3} n \frac{m \overline{v^2}}{2}
This is a first non-trivial result of the kinetic theory because it relates pressure, a macroscopic property, to the average (translational) kinetic energy per molecule {1 \over 2} m\overline{v^2} which is a microscopic property.

Temperature and kinetic energy

From the ideal gas law
\displaystyle PV = N k_B T
 (1)
where \displaystyle k_B is the Boltzmann constant, and \displaystyle T the absolute temperature,
and from the above result PV = {Nmv_{rms}^2 \over 3}
we have \displaystyle N k_B T = \frac {N m v_{rms}^2} {3}
then the temperature \displaystyle T takes the form
\displaystyle T = \frac {m v_{rms}^2} {3 k_B}
 (2)
which leads to the expression of the kinetic energy of a molecule
\displaystyle \frac {1} {2} mv_{rms}^2 = \frac {3} {2} k_B T
The kinetic energy of the system is N time that of a molecule K= \frac {1} {2} N m v_{rms}^2
The temperature becomes
\displaystyle T = \frac {2} {3} \frac {K} {N k_B}
 (3)
Eq.(3)1 is one important result of the kinetic theory: The average molecular kinetic energy is proportional to the absolute temperature.
From Eq.(1) and Eq.(3)1, we have
\displaystyle PV = \frac {2} {3} K
 (4)
Thus, the product of pressure and volume per mole is proportional to the average (translational) molecular kinetic energy.
Eq.(1) and Eq.(4) are called the "classical results", which could also be derived from statistical mechanics; for more details, see [1].
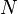Since there are \displaystyle 3N degrees of freedom (dofs) in a monoatomic-gas system with \displaystyle N particles, the kinetic energy per dof is
\displaystyle \frac {K} {3 N} = \frac {k_B T} {2}
 (5)
In the kinetic energy per dof, the constant of proportionality of temperature is 1/2 times Boltzmann constant. This result is related to the equipartition theorem.
As noted in the article on heat capacity, diatomic gases should have 7 degrees of freedom, but the lighter gases act as if they have only 5.
Thus the kinetic energy per kelvin (monatomic ideal gas) is:
  • per mole: 12.47 J
  • per molecule: 20.7 yJ = 129 μeV
At standard temperature (273.15 K), we get:
  • per mole: 3406 J
  • per molecule: 5.65 zJ = 35.2 meV

Number of collisions with wall

One can calculate the number of atomic or molecular collisions with a wall of a container per unit area per unit time.
Assuming an ideal gas, a derivation[2] results in an equation for total number of collisions per unit time per area:
A = \frac{1}{4}\frac{N}{V} v_{avg} = \frac{\rho}{4} \sqrt{\frac{8 k T}{\pi m}} \frac{1}{m}. \,

RMS speeds of molecules

From the kinetic energy formula it can be shown that
v_{rms}^2 = \frac{3RT}{\mbox{molar mass}}
with v in m/s, T in kelvins, and R is the gas constant. The molar mass is given as kg/mol. The most probable speed is 81.6% of the rms speed, and the mean speeds 92.1% (distribution of speeds).
 
Search Engine